Question

Find the linear approximation of f(x) = ln x at x = 1 and use it to estimate In(1.46).L(x) =In 1.46

Answer 1

`\begin{gathered} L(x)=x-1 \\ \ln1.46=0.46 \end{gathered}`

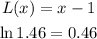
Step-by-step explanation

We want to find the linear approximation of the function at x = 1:

`f(x)=\ln x`

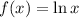
First, we have to find the equation of the tangent line to the function at x = 1:

`\begin{gathered} f(1)=\ln(1) \\ f(1)=0 \end{gathered}`

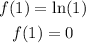
Now, find the derivative of the function at x = 1:

`\begin{gathered} f^(\prime)(x)=(1)/(x) \\ \Rightarrow f^(\prime)(1)=(1)/(1) \\ f^(\prime)(1)=1 \end{gathered}`

Now, find the equation of the line using the point-slope method:

`y-y_1=m(x-x_1)`

Therefore, we have:

`\begin{gathered} y-0=1(x-1) \\ y=x-1 \end{gathered}`

Hence, the linear approximation of f(x) at x = 1 is:

`L(x)=x-1`

To find the estimate of ln(1.46), substitute 1.46 for x in the equation above and simplify:

`\begin{gathered} \ln1.46=L(1.46)=1.46-1 \\ \ln1.46=0.46 \end{gathered}`

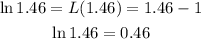
That is the answer.