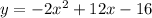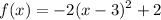
Required:
a. vertex
b.the directions of the parabola.
c. the width of the parabola.
d.the axis of symmetry
e.the x-intercepts
f.the y-intercepts
g.the number of solutions.
h.the standard form of the equation
Solution:
The vertex form of the equation of a parabola is
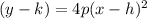
where h and k are the coordinates of the vertex.
a) Manipulating this function to the vertex form:
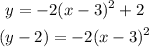
Here, h = 3 and k = 2 . Thus the vertex is at V ( 3, 2 )
b) If the x is squared, the parabola is vertical (opens up or down). If the y is squared, it is horizontal (opens left or right). If a is positive, the parabola opens up or to the right. If a is negative, it opens down or to the left.
In this function x is squared and a is equal to -2 . Therefore, the parabola opens downward.
c) The focal width of the parabola is equivalent to 4p. From the vertex form of the equation, we can tell that 4p is 2. Thus, the width of the parabola is 2 units
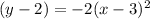
h) THE STANDARD FORM OF THE EQUATION
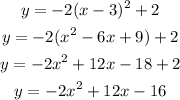
d) The axis of symmetry is given by x = -b / 2a
In the above equation of the parabola, a = -2 and b = 12. Thus x = -b / 2a = - (12) / 2 ( -2 ) = -12 / - 4 = 3
The axis of symmetry is x = 3
THE INTERCEPT FORM y = a(x - r)(x - s), where r and s are the x-intercepts on the graph. It tell us if there are two x-intercepts, one x-intercept or no x-intercepts.
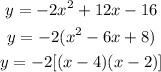
e) From the intercept form of the equation of the parabola, we can tell that r = + 4 and s = + 2. Therefore , the x - intercepts of the parabola are at x = 4 and x = 2
f) The y -intercept is the point at which the parabola crosses the y -axis where x is zero. In the given funxction , if we let x be equal to zero then y is :
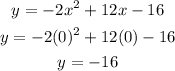
The y -intercept of the parabola is y = -16 .
g) A parabola can have one, two, or no solutions. The solution of a parabola refers to the points where the graph does intersect with the x-axis. In the given function , there are two points where the parabola intersects the x-axis ( refer to e ) at x = 4 and x = 2. Therefore, the given parabola has two solution.
h) The standard equation of a parabola is
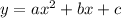
The standard form of the given function is : ( refer to the deriviation above, after c )
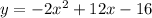
Answers:
a) V ( 3, 2 )
b) The parabola opens downward
c) The width of the parabola is 2 units
d) The axis of symmetry is x = 3
e) The x - intercepts of the parabola are at x = 4 and x = 2
f) The y -intercept of the parabola is y = -16
g) The given parabola has two solutions.
h) The standard form of the given function is