Question

Drag the tiles to the correct boxes to complete the pairs. Not all tiles will be used.Match each table to its corresponding explicit formula.

Answer 1

Recall that the pattern for the formula of an exponential function is:

`f(x)=ab^x`

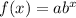
where a = the initial value at x = 0, and b is the growth/decay factor in the function.

In the given options, we can rewrite the pattern of the formula as:

`f(n)=ab^(n-1)`

Please note that we have subtracted 1 from "n" since the initial value in the table starts at n = 1 to make the exponent equal to zero when using the initial value in the table.

Now, let's start identifying the explicit formula for the first sequence or the first table.

In the table, we see that the initial value is 2, hence, in the formula, a = 2.

As we have noticed too, as the value of "n" increases by 1, the value of f(n) is multiplied by a factor of 4. Therefore, b = 4.

Plugging into the formula the value of a = 2 and b = 4, the explicit formula of the first table is:

`f(n)=2\cdot(4)^(n-1)`

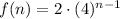
Moving on to the second table, its initial value is 3. Hence, a = 3. As the value of "n" increases by 1, the value of f(n) is multiplied by a factor of 2. Hence, b = 2.

Plugging in a = 3 and b = 2 to the formula, the explicit formula of the second table is:

`f(n)=3\cdot(2)^(n-1)`

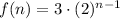
Lastly, for the third table, the initial value is 2. Hence, a = 2.

In addition, we see that as the value of "n" increases by 1, the value of f(n) in table 3 is multiplied by a factor of 6. Hence, b = 6.

Plugging in a = 2 and b = 6 to the formula, the explicit formula of the third table is:

`f(n)=2\cdot(6)^(n-1)`

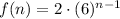
To summarize, here are the corresponding explicit formulas that matched to each table.