Solution:
We can use the following formula:
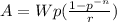
Here A is the initial amount at the account;
W is the monthly withdrawn value;
r is the nominal monthly percentage.
n is the number of withdrawing periods (months, in this case).
Now, in this case, we have the following data:
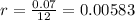
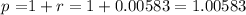
and the number of payment periods (= the number of months) is
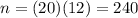
Applying these data to the formula given at the beginning of this explanation, we obtain:
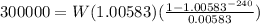
this is equivalent to:
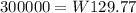
solving for W, we get:
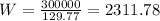
Thus, the correct solution is:
You will be able to withdraw about $2311.78 every month for 20 years.