Answer:
The beach house with the highest rate per night is House 2.
They charge $249 per night
Step-by-step explanation:
Given that the graph represent the rate at which House 1 charges;
We need to derive the equation for house 1.
Recall that the slope-intercept equation of a straight line can be represented by;

where;
m = slope
b = y-intercept
Fro the given graph the y-intercept is at y=200, so;
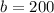
we can also calculate the slope m using the formula;

Substituting the coordinates on the graph;
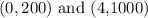
we have;

Therefore, we can write the equation for House 1 as;
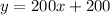
So, the equation for each house is;
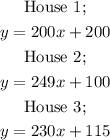
where y is the total cost, x is the number of nights.
From the three equations, the beach house with the highest rate is House 2.
They charge $249 per night