Step-by-step explanation
The sum of the three internal angles of a triangle is equal to 180°. Then for a triangle with angles A, B and C we get:
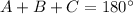
Considering the sides of the triangle are a, b and c and they are opposite to angles A, B and C respectively the law of sines states that:
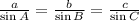
Now let's use these properties to find the other two possible triangles. From the law of sines we get:
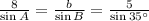
We can build an equation for A:
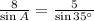
We can invert both sides of this equation:
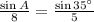
And we multiply both sides by 8:
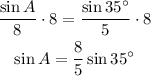
We can use the arcsin function to find A:
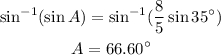
However that's not the only possible value of A. A can be acute (smaller than 90°) or obtuse (greater than 90°). This is the value of A if it's acute. In order to find the value of A when it's obtuse we have to find an angle with a sine that is equal to that of A.
It's important to remember that for any angle x in the first quadrant [0°,90°) there's another angle in the second quadrant [90°,180°) that has the same sine. This angle is given by:
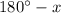
So the obtuse value of A is:
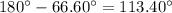
Now let's find B and b in each case.
First if A=66.60° the sum of A, B and C is:
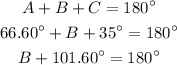
Then we substract 101.6° from both sides:
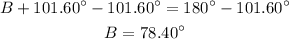
Then the law of sines looks like this:
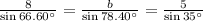
So we have the following equation for b:
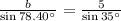
We multiply both sides by sin(78.40°) and we find b:
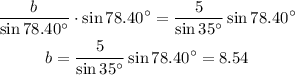
Now let's do the same for the obtuse value of A: 113.40°. The sum of the internal angles is:

We substract 148.40° from both sides:

Then the law of sines is:

Then we get this equation for b:
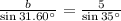
And we multiply both sides by 31.60°:
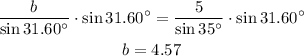
Answers
The answers for triangle 1 are:
A = 66.60°
B = 78.40°
b = 8.54
The answers for triangle 2 are:
A = 113.40°
B = 31.60°
b = 4.57