Question

PROBABILITY (Chapter 10)223EXERCISE 10B1 Jose surveyed the length of TV commercials in seconds.Estimate, to 3 decimal places, the probability that a randomlychosen TV commercial will last:a 20 to 39 secondsb more than a minutec between 20 and 59 seconds inclusive.Length Frequency0 - 19 1720 - 39 3840 - 59 1960+4

Answer 1

The probability of an event is expressed as

`Pr(\text{event)}=\frac{\text{Number of desired outcome}}{Number\text{ of possible outcome}}`

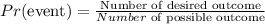
Given the survey as shown below:

a) Probability that the chosen TV commercial will last 20 to 39 seconds.

Thus,

`\begin{gathered} Pr(20-39\text{ seconds)=}\frac{frequency\text{ of 20-30 seconds}}{total\text{ frequency}} \\ =(38)/(78) \\ =0.4871794872 \\ \therefore Pr(20-39\text{ seconds)}\approx0.487\text{ (3 decimal places)} \end{gathered}`

Hence, the probability that the chosen TV commercial will last 20 to 39 seconds is 0.487.

b) Probability that the chosen TV commercial will last more than a minute.

Thus,

`\begin{gathered} Pr(\text{more than a minute)=Pr(60+)=}(4)/(78) \\ =0.05128205128 \\ \Rightarrow Pr(\text{more than a minute)}\approx0.051\text{ (3 decimal places)} \end{gathered}`

Hence, the probability that the chosen TV commercial will last more than a minute.is 0.051.

c) Probability that the chosen TV commercial will last between 20 and 59 seconds inclusive.

Thus,

`\begin{gathered} Pr(20\text{ and 59 seconds inclusive)=Pr(20-39) and Pr(40-59)} \\ \text{where} \\ \text{Pr(20-39)=}(38)/(78) \\ \text{Pr(40-59)=}(19)/(78) \\ \text{thus,} \\ Pr(20\text{ and 59 seconds inclusive)=}(38)/(78)*(19)/(78) \\ =\: 0.1186719264 \\ \Rightarrow Pr(20\text{ and 59 seconds inclusive)}\approx0.119\text{ (3 decimal places)} \end{gathered}`

Hence, the probability that the chosen TV commercial will last between 20 and 59 seconds inclusive is 0.119.