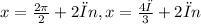ANSWER
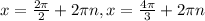
Step-by-step explanation
To solve this equation, first, we have to subtract 4 from both sides of the equation,
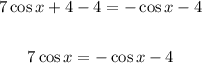
Then, add cos x to both sides,
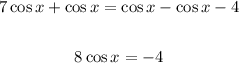
Divide both sides by 8,
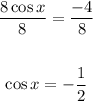
If we look at the unit circle, we will find that there are two angles whose cosine is -1/2,
And these two angles only repeat every 2π radians.
Hence, the solutions to this equation are: