Question

A researcher wishes to conduct a study of the color preferences of new car buyers. suppose that 50% of this population prefers the color green. if 16 buyers are randomly selected, what is the probability that exactly 9 buyers would prefer green? round your answer to four decimal places.

Answer 1

To solve this question, use the Binomial probability formula.

The formula is given by

`^nC_xp^x(1-p)^(n-x)`

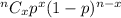
Where:

n = the number of trials

x = the sample we aim to try

p = the probability of success

In this question:

n = 16

x = 9

p = 0.5

Substituting in the equation:

`\begin{gathered} ^nC_xp^x(1-p)^(n-x) \\ ^(16)C_9*0.5^9(1-0.5)^(16-9) \\ \end{gathered}`

And the combination formula:

`^nC_x=(n!)/((n-x)!*x!)`

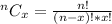
Then:

`\begin{gathered} (16!)/((16-9)!*9!)*0.5^9(1-0.5)^(16-9) \\ (16!)/(7!*9!)*0.5^9*0.5^7 \\ 11440*0.00195*0.0078 \\ =0.1746 \end{gathered}`

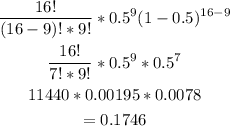
Answer: The probability is 0.1746.