Question

1-solve2-what is the discriminant value from the problem?step by step please

Answer 1

1.

`x_{}=\frac{-2+\sqrt[]{104}i}{18},\frac{-2-\sqrt[]{104}i}{18}`

2.

-104

Explanation:

We have the following equation:

`9x^2+2x=-3`

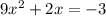
The first thing is to express the equation in its general form, like this:

`9x^2+2x+3=0`

In this way we can determine a (coefficient of the quadratic term), b (coefficient of the non-quadratic term x) and c (constant or independent term)

In this case:

a = 9

b = 2

c = 3

We calculate the determinant as follows:

`\Delta=b^2-4ac`

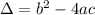
We substitute and calculate the discriminant:

`\begin{gathered} \Delta=2^2-4\cdot9\cdot3 \\ \Delta=4-108 \\ \Delta=-104 \end{gathered}`

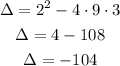
Since the determinant is negative, the solution of the equation is 2 different complex roots.

We calculate them by means of the general formula of quadratic equations:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{ we replacing} \\ x=\frac{-2\pm\sqrt[]{2^2-4\cdot9\cdot3}}{2\cdot9} \\ x=\frac{-2\pm\sqrt[]{-104}}{18} \\ x_1=\frac{-2+\sqrt[]{104}i}{18} \\ x_2=\frac{-2-\sqrt[]{104}i}{18} \end{gathered}`