Given the parallelogram ABCD, draq diagonal AC
From the parallelogram above, it can observed that line BCis parallel to line AD. Also, the line AB is parallel to line DC
The diagonal AC is a transversal to the two parallel lines BC and line AD
In the triangles ABC and triangle CDA,
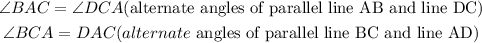
From the two triangles ABC and CDA, line AC and line CA are common to them
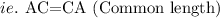
It can be deduced that triangle ABC is congruent to triangle CDA
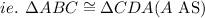
Hence, AB≅CD and BC≅DA (Matching sides of congruent triangles ABC and triangles CDA)