Question

Solve the following system of equations -16y = 4 4x+ 27y=11 Enter the solution as an ordered pair:(

Answer 1

Given the below equations;

`\begin{gathered} -16y=4 \\ \\ 4x+27y=11 \end{gathered}`

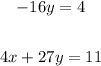
We can solve this by using the substitution method, we'll go ahead and find y in the 1st equation and substitute the value of y into the 2nd equation to find x;

To find y in the 1st equation;

`\begin{gathered} -16y=4 \\ -(16y)/(16)=(4)/(16) \\ -y=(1)/(4) \\ \therefore y=-(1)/(4) \end{gathered}`

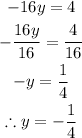
To find x,let's substitute the value of y into the 2nd equation;

`\begin{gathered} 4x+27(-(1)/(4))=11 \\ 4x-(27)/(4)=11 \\ 16x-27=44 \\ 16x=44+27 \\ 16x=71 \\ (16x)/(16)=(71)/(16) \\ x=(71)/(16) \\ \end{gathered}`

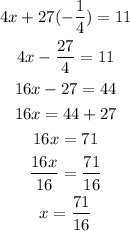
Therefore, the solution is (71/16, -1/4) or (4.44, 0.25) in decimal.