Given data:
* The height of the stone is h = 50 m.
* The initial horizontal speed of the stone is v = 4 m/s.
Solution:
By the kinematics equation along the vertical direction, the time taken by the stone to reach the ground is,
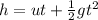
where u is the initial vertical speed of the stone,
The initial vertical velocity of the stone is zero, thus,
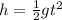
where g is the acceleration due to gravity,
Substituting the known values,
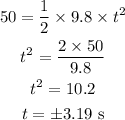
Neglecting the negative value of time,
Thus, the time taken by the stone to reach the ground is 3.19 s.
Hence, option D is the correct answer.