Question

Now try this Take point A (3,5) and perform the following transformations (in order!) (1) Rotate it 2709 counterclockwise around the origin (2) Translate it by the rule T(2,-2) (3) Reflect it over the x-axis Just type the answer with no label*

Answer 1

We have to apply transformations to point A=(3,5).

First, we have to rotate 270° counterclockwise, which is the same to rotate 90° clockwise, so the transformation is:

`\begin{gathered} (x,y)\to(-y,x) \\ \text{For point A(3,5) the rotation is:} \\ A(3,5)\to A^(\prime)(-5,3) \end{gathered}`

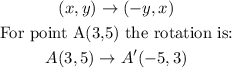
Then transtalate by the rule T(2,2), this means:

`\begin{gathered} T_((2,2))(x,y)=(x+2,y+2) \\ So,\text{ for point A'(-5,3):} \\ A^(\doubleprime)=T_((2,2))(-5,3)=(-5+2,3+2)=(-3,5) \end{gathered}`

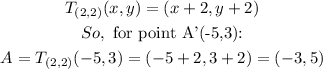
Finally we have a reflection on x-axis, so:

`\begin{gathered} (x,y)\to(x,-y) \\ \text{For point A''(-3,5):} \\ A^(\doubleprime)(-3,5)\to A^(\doubleprime)^(\prime)(-3,-5) \end{gathered}`

The final point after all the transformations is A'''(-3,-5)