Trigonometric Ratios
A right triangle has one angle of 90° and two acute angles. There are special proportions between the side lengths called the trigonometric ratios.
All the trigonometric ratios in a right triangle are positive.
We need to use some trigonometric identities to find the other five ratios, given one of them:
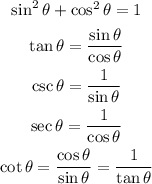
We are given:
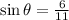
From the first identity, solve for the cosine:
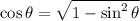
Substituting:
![\begin{gathered} \cos \theta=\sqrt[]{1-((6)/(11))^2} \\ \cos \theta=\sqrt[]{1-(36)/(121)} \\ \cos \theta=\sqrt[]{(121-36)/(121)} \\ \cos \theta=\sqrt[]{(85)/(121)} \\ \cos \theta=\frac{\sqrt[]{85}}{11} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jseuopgt3mctpkt63xac931gj3vcxcxi20.png)
Calculate the tangent:
![\begin{gathered} \tan \theta=\frac{(6)/(11)}{\frac{\sqrt[]{85}}{11}} \\ \tan \theta=\frac{6}{\sqrt[]{85}} \\ \text{Rationalizing:} \\ \tan \theta=\frac{6}{\sqrt[]{85}}\cdot\frac{\sqrt[]{85}}{\sqrt[]{85}} \\ \tan \theta=\frac{6\sqrt[]{85}}{85} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yleougjh541g4rzgp3rstkqm8jtcbxpgr7.png)
Calculate the cosecant:
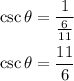
Calculate the secant:
![\begin{gathered} \sec \theta=\frac{1}{\frac{\sqrt[]{85}}{11}} \\ \sec \theta=\frac{11}{\sqrt[]{85}} \\ \text{Rationalizing:} \\ \sec \theta=\frac{11}{\sqrt[]{85}}\cdot\frac{\sqrt[]{85}}{\sqrt[]{85}} \\ \sec \theta=\frac{11\sqrt[]{85}}{85} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/eps1k4sk9dizwkdkt0826aj292cxplicos.png)
Finally, calculate the cotangent:
![\begin{gathered} \cot \theta=\frac{\frac{\sqrt[]{85}}{11}}{(6)/(11)} \\ \cot \theta=\frac{\sqrt[]{85}}{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qb9n2coxnef3xuq84t4abafnsfhauajuyd.png)