Question

A roller-coaster goes over an 9 m tall hill then approaches a 27 m hill. What is theminimum velocity the roller-coaster would need when going over the 9 m hill tomake it to the top of the 27 m hill?

Answer 1

Given data:

* The height of the initial hill is 9 m.

* The height of the final hill is 27 m.

Solution:

The amount of potential energy acquired by the roller coaster by reaching top of 27 m hill from the 9 m hill is,

`U=mg(h_f-h_i)`

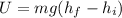
where m is the mass of the roller coaster, g is the acceleration due to gravity, h_f is the final height of hill, and h_i is the initial height of the hill,

Substituting the known values,

`\begin{gathered} U=m*9.8*(27-9) \\ U=m*9.8*18 \\ U=m*176.4 \end{gathered}`

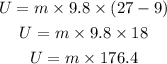
The kinetic energy of the roller coaster at the start of motion from 9 m hill is,

`K=(1)/(2)mv^2`

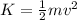
where v is the velocity of the roller coaster at the start of the motion,

According to the law of conservation of energy,

`\begin{gathered} K=U \\ (1)/(2)mv^2=176.4* m \\ v^2=2*176.4 \\ v^2=352.8 \\ v=18.78\text{ m/s} \end{gathered}`

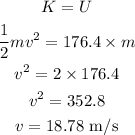
Thus, the minimum value of the velocity required to move the roller coaster to the top of 27 m hill from the 9 m hill is 18.78 m/s.