Question

A rocket is thrown upward from the top of a tall building

Answer 1

The Solution:

The given function that describes the height of the rocket is

`h=-16t^2+48t+160`

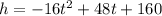
a. We are asked to find the time (t) it takes for the rocket to reach a height of 160 feet.

We shall substitute 160 feet for h in the given function.

`\begin{gathered} 160=-16t^2+48t+160 \\ 0=-16t^2+48t \end{gathered}`

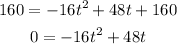
Factorizing, we get

`\begin{gathered} 16t(-t+3)=0 \\ 16t=0\text{ or -t+3=0} \\ t=0\text{ or t=3} \end{gathered}`

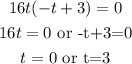
So, it took the object 3 seconds to reach a height of 160 feet.

b.

We are required to find the time(t) it will take the object to hit the ground.

For the object to hit the ground, the height has to be zero (0).

So, we shall substitute 0 for h in the given function.

`0=-16t^2+48t+160`

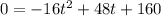
Solving the above quadratic equation by Factorization Method, we have

`\begin{gathered} 16t^2-48t-160=0 \\ t^2-3t-10=0 \\ t^2-5t+2t-10=0_{} \end{gathered}`
`\begin{gathered} t(t-5)+2(t-5)=0 \\ (t+2)(t_{}-5)=0 \\ t+2=0\text{ or t-5=0} \\ t=-2\text{ or t=5} \end{gathered}`

Since, the time (t) cannot be negative, we discard -2.

So, the time it will take the object to reach the ground is 5 seconds.