Given:
Find-:
Dimensions of the cardboard
Explanation-:
The volume of a quadrangular prism is:

The length is 12 more than the width is:
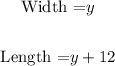
Hight is 6.
So the Area is:
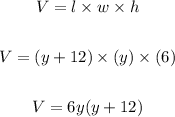
Given that volume is 2958 so,
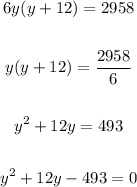
Solve the quadratic equation is:
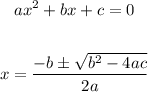
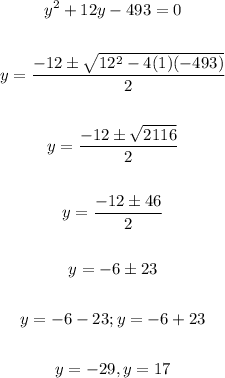
A negative value is not considered because sides are always positive so y is 17.
So the width is 17 and length is:
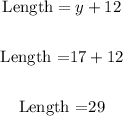
So dimensions are 29 in. by 17 in.