Given:
The system of equation is,
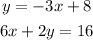
Simplify both the equation,

and,
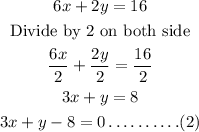
It is observed that both the equations of line are same. moreover the lines completely overlap.
It shows the system has infinitely many solutions.
Now check the points (-5,0) ,(7, -13),(1,8),(-2, 14) represents the solution of the given system of equation.
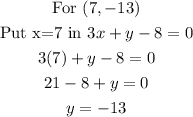
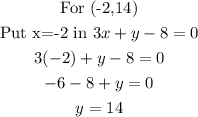
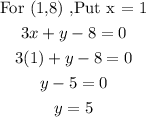
This is not the solution of the given system of equations as it does not satisfy the equation.
Also point ( -5,0) is also not the solution of the equation.
Answer:
The system of equation has infinitely many solution and point (7, -13) and (-2, 14) is the solution.