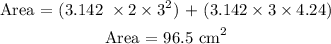Question

A solid metal spinning top is constructed by joining a hemispherical top to a cone-shaped base. The radius of both thehemisphere and the base of the cone is 3 cm. The volume of the cone is half that of the hemisphere. Find the following tothree significant figures:a. The volume of the hemispherical top = 56.5cm^3b. The height of the cone-shaped base = 3cm^2C. The outer surface area of the entire spinning top including all pieces

Answer 1

a) The volume of the hemisphere is 56.5 cm^3

b) The height of the cone is 3 cm

c) The outer surface area of the shape is 96.5 cm^2

HERE, we want to calculate the given measures

a) The volume of the hemispherical top

To calculate this, we use the formula for the volume of a hemisphere

Mathematically, we have this as follows;

`V\text{ = }(2)/(3)\text{ }*\text{ }\pi\text{ }* r^3`

From the question, we have the radius of the hemisphere as 3cm

We have this as;

`V\text{ =}(2)/(3)*3.142*3^3=56.5cm^3`

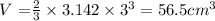
b) We want to calculate the height of the cone-shaped base

From the question, we are told that the volume of the cone is half that of the hemisphere;

The volume of the cone is thus;

`V\text{ = }(56.5)/(2)=28.25cm^3`

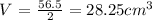
Mathematically, we have the volume of a cone as follows;

`V\text{ = }(1)/(3)*\pi\text{ }* r^2* h`

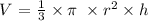
Substitute the value of the volume and the value of the r so that we can get the height

We have this as;

`\begin{gathered} 28.25\text{ = }(1)/(3)\text{ }*\text{ 3.142 }*3^2\text{ }*\text{ h} \\ \\ h\text{ = }\frac{28.25}{3.142\text{ }*\text{ 3}}\text{ = 2.997 which is 3 cm} \end{gathered}`

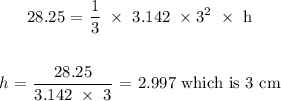
c) Here, we want to get the outer surface area of the spinning top and the pieces

Mathematically, we have that as the sum of the area of the hemisphere plus that of the cone

We have that as;

`A\text{ = (2}*\pi* r^2)\text{ + }\pi rl`

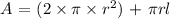
Now, you will notice that we do not use the full area of the cone

This is because we have the hemisphere taking this up already and we only need the surface area of the hemisphere.

We do not find the area of the circular base of the cone

We also can notice the l term in the area of the cone

The l term stands for the slant height of the cone

The slant height can be calculated using the Pythagoras' theorem, with the base of the cone and its height serving as the other sides and the slant height serving as the hypotenuse. The Pytahgoras' theorem states that the square of the hypotenuse (slant height) equals the sum of the squares of the two other sides (base and height of the cone)

So, we have the slant height as;

`\begin{gathered} l\text{ = }\sqrt[]{3^2+3^2} \\ l\text{ = }\sqrt[]{18} \\ l\text{ = 4.24 cm} \end{gathered}`

So applying these to the area formula we deduced above, we have;

`\begin{gathered} \text{Area = (3.142 }*2*3^2)\text{ + (3.142}*3*4.24) \\ \text{Area = 96.5 cm}^2 \end{gathered}`