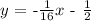Given the equation:
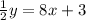
Rewrite the equation in slope intercept form:
y = mx + b
Multiply both through by 2
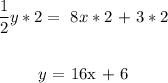
The slope of this line is 16.
therefore, the slope of the line perperndicular to it will be it's inverse:
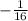
The perpendicular line has the points:
(x, y) ===> (-8, 0)
We have:
y = mx + b
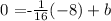
Solve for b which is the y-intercept:
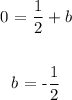
Since the y intercept is -½
slope = -1/16
The equation of the line in point slope form:
(y - y1) = m(x - x1)
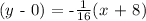
Therefore, the equation of the perpendicular line in slope intercept is: