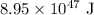Question

Models indicate that the gravitational-wave signal came from the merger of two black holes with masses of 31 Msun and 38 Msun, a merger that resulted in a single black hole with a mass of 64 Msun. The difference in total mass between the start and finish of the merger corresponds to the amount of energy carried away in the form of gravitational waves. Use Einstein’s formula E = mc^2 to calculate the amount of energy. Express your answer to two significant figures and include the appropriate units.

Answer 1

The total mass of two black holes is given as,

`m^(\prime)=m_1+m_2`

Plug in the known values,

`\begin{gathered} m^(\prime)=31M_(sun)+38\text{ }M_(sun) \\ =69\text{ }M_(sun) \end{gathered}`

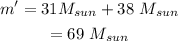
The loss of mass can be expressed as,

`m=m^(\prime)-m_0`

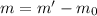
Substituting known values,

`\begin{gathered} m=69\text{ }M_(sun)-64\text{ }M_(sun) \\ =5M_(sun) \end{gathered}`

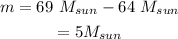
The amount of energy carried away can be expressed as,

`E=mc^2`

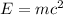
Substitute the known values,

`\begin{gathered} E=(5)(1.989*10^(30)\text{ kg)(}3*10^8m/s)^2(\frac{1\text{ J}}{1kgm^2s^(-2)}) \\ =8.95*10^(47)\text{ J} \end{gathered}`

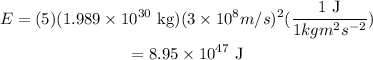
Thus, the amount of energy carried away is

`8.95*10^(47)\text{ J}`