Question

Three vertices of GHIJ are G(0,0), H(2, 3), and J(6, 1). Use the grid to the right to complete Problems 10–16. 10. Plot vertices G, H, and J on the coordinate plane. 11. Find the rise (difference in the y-coordinates) from 3 G to H. 0 12. Find the run (difference in the x-coordinates) from Gto H. 13. Using your answers from Problems 11 and 12, add the rise to the y-coordinate of vertex J and add the run to the x-coordinate of vertex J. The coordinates of vertex / are 14. Plot vertex I. Connect the points to draw GHIJ. 15. Check your answer by finding the slopes of IH and JG. slope of IH slope of JG 16. What do the slopes tell you about IH and JG?

Answer 1

10. We will graph the coordinates of the vertices in the plane:

11. From G to H, we can find the ris by looking at the difference between their y-coordinates:

`y_h-y_g=3-0=3`

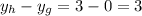
The rise is 3.

12. The difference in x coordinates is:

`x_h-x_g=2-0=2`

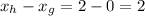
The run is 2.

13. If we add the rise and the run to J, we get the coordinates of I:

`\begin{gathered} x_i=x_j+2=6+2=8 \\ y_i=y_j+3=1+3=4 \\ I=(8,4) \end{gathered}`

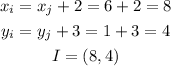
14. We add I(8,4) to the plot and connect the points:

15. We have to calculate the slopes of IH and GJ:

`m_(ih)=(y_i-y_h)/(x_i-x_h)=(4-3)/(8-2)=(1)/(6)`
`m_(jg)=(y_j-y_g)/(x_j-x_g)=(1-0)/(6-0)=(1)/(6)`

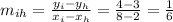
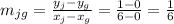
Both slopes have the same value: m_ih = m_jg = 1/6.

16. As the slopes are equal, that tells us that the segments are parallel.