The slope can be described as the rise (change on y-axis) of a function over the run (change on x-axis).
When the change in the rise is negative and the change in the run is positive, we obtain the following:
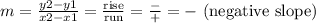
We can see this in the first function image:
This slope is negative then.
In the second function, the rise is 0 (no change in the y-axis) and the run is positive. Then:
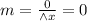
This slope is zero.
In the third function, the rise is positive and the run is zero (no change in the x-axis), then the slope is given by:
![m=(\wedge y)/(0)=\text{undefined}]()
This slope is undefined.
In the last function, the rise increases and the run increases, then the slope is positive.