ANSWER
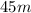
Step-by-step explanation
To find how far the student lands, we first have to find the time of flight using the equation that governs vertical motion:
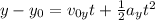
where y0 = initial height; y = final height; voy = initial velocity in the y direction; t = time; ay = -g; g = acceleration due to gravity
From the question, we have that:
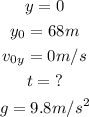
Therefore, we have that:
![\begin{gathered} 0-y_0=0-(1)/(2)gt^2 \\ \Rightarrow t^2=(2y_0)/(g) \\ t=\sqrt[]{(2y_0)/(g)} \\ t=\sqrt[]{(2\cdot68)/(9.8)} \\ t=3.73\text{ seconds} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/r9xati3oxe1l7a2df9sx7d8e5w3l4g3evc.png)
Now, we can apply the equation that governs horizontal motion to find the distance from the base of the cliff:
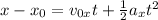
where x = distance from bottom of cliff; x0 = starting position; v0x = initial velocity in the x-direction; ax = acceleration in the x-direction
From the question, we have that:
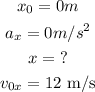
Therefore, the distance of the student from the base of the cliff is:
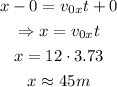
That is the answer (to 2 significant figures).