Answer:
Given that,
When Ayla plays darts the chances that she hits bulls eye is 0.5.
To find: The chances that three darts fired in succession will all hit bulls eye.
Consider p be the probability of success.
Here,
p=0.5
q be the probability of failure,
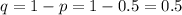
By binomial distribution, we have that,
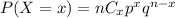
where n is the number of times the event is repeated and x is the number of favorable outcomes.
Here, n=3, we get
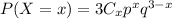
Here, x=3, we get,
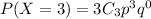
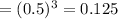
The required probability is 0.125.
2)To find the probability that none will hit.
Here, x=0, substitute the value in P(X=x), we get
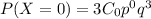
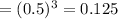
The required probability is 0.125.
3) To find the probability that a least one dart will hit.
Here, to find P(X>0), we get,
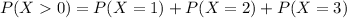
Substitute the values we get,
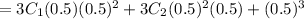
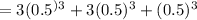
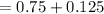
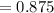
The required probability is 0.875