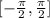To determine the restriction of the domain of the function tan(x), let us analyze its definition:
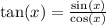
Because cos(x) goes to zero for values of x equal to ±π/2, for these values we have the limits, in the sense of edge, of the function. After this point tan(x) starts to repeat the values.
Because the edges are given by ±π/2, and the function is not defined in the point, because it becomes a division by 0, we can solve the first part of the problem:
The domain of f(x) = tan( x) is restricted to:
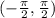
so that the inverse of that function exists. This means that all functional values of f(x) = tan^(-1)( x ) are on the interval: