ANSWERS
(a) 5.53 x 10⁻³ m
(b) 0.016 m
Step-by-step explanation
Given:
• The mass of the block, m = 0.843 kg
,
• The spring's force constant, k = 187 N/m
,
• The static coefficient of friction between the object and the horizontal surface, μs = 0.125
Find:
• (a) ,The distance, x, the spring can be stretched without moving the mass.
,
• (b), If the oscillation amplitude is 2x and the kinetic coefficient of friction is μk = 0.0846, find the total distance it travels before stopping, d.
(a) The maximum distance the spring can be stretched without moving the mass is the distance at which the static friction force is equal to the spring force - this we know it by Newton's second law of motion,
This is,
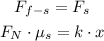
The normal force, since the block is not moving vertically, is equal to the weight of the object,
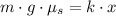
Solving for x and replacing the known values,
![x=\frac{m\cdot g\operatorname{\cdot}\mu_s}{k}=\frac{0.843kg\operatorname{\cdot}9.81m/s^2\operatorname{\cdot}0.125}{187N/m}\approx5.53\cdot10^(-3)m]()
Hence, the spring can be stretched to a maximum of 5.53 x 10⁻³ m without moving the mass.
(b) The oscillation amplitude is twice the distance found in part (a), so the amplitude is about A = 0.011 m. When the spring is stretched to this amplitude, it stores energy given by,
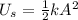
This energy will be equal to the work done by the kinetic friction between the object and the surface, which is the product of the kinetic force and the distance the mass travels for - this is what we want to find,
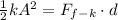
The kinetic friction force is similar to the static friction force: it is the product between the normal force - which in this case is equal to the weight of the object, and the kinetic coefficient of friction,
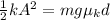
Solving for d and replacing with the known values we have,
![d=\frac{kA^2}{2\cdot m\operatorname{\cdot}g\operatorname{\cdot}\mu_k}=\frac{187N/m\cdot0.011^2m^2}{2\operatorname{\cdot}0.843kg\operatorname{\cdot}9.81m/s^2\operatorname{\cdot}0.0846}\approx0.016m]()
Hence, the mass will travel a distance of 0.016 m before stopping.