Question

The graph shows the amounts customers pay for x pounds of cheese at a deli counter. Customers pay a certain price per pound up to exactly 5 pounds If a costumer buys more than 5 pounds, then the price pound for the entire purchase is discounted

Answer 1

Here, we have a piece wise function to define

We start with the horizontal line from the origin

Generally, the equation of a straight line is;

`y\text{ = mx + b}`

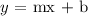
where m is the slope of the line and b is the y-intercept

As we can see, the line starts from the origin and that means the line has a y-intercept equal to zero

Now, we can see that; y = mx is a probable equation for the line

So to get the value of m, we need two points in which we can apply the slope equation

The two points lying on the line that we want to select are (0,0) and (5,25)

By this, we have the slope of the equation as;

`\begin{gathered} m\text{ = }(y_2-y_1)/(x_2-x_1) \\ (x_1,y_1)\text{ = (0,0)} \\ (x_2,y_2)\text{ = (5,25)} \\ m\text{ = }(25-0)/(5-0) \\ m\text{ = }(25)/(5) \\ m\text{ = 5} \end{gathered}`

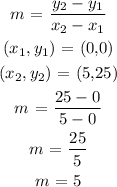
So, we have the first equation in the piece-wise function as;

`y\text{ = 5x}`

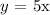
Now, we have the domain as;

`0\text{ }Now, for the second piece-wise function, we have to select two points to use<p></p><p>We have the selected points as (10,40) and (5,20)</p><p></p><p>So using the slope equation, we have;</p><p></p>[tex]m\text{ = }(40-20)/(10-5)\text{ = }(20)/(5)\text{ = 4}`

For the y-intercept, we make a substitution;

`\begin{gathered} y\text{ = mx + c} \\ y\text{ = 4x + c} \\ 40\text{ = 4(10) + c} \\ 40\text{ =40 + c} \\ c\text{ = 40-}40 \\ c\text{ = }0 \end{gathered}`

So, we have the equation for the second line as;

`y\text{ = }4x`

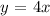
We have the domain as;

`x\text{ }>\text{ 5}`

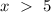
What this mean is that customers who by up to 5 pounds pay $5 per pound

Customers who buy more than 5 pounds pay $20 for the first 5 pounds. They pay $4 per pound for each pound over 5 pounds