We are going to apply the Triangle Inequality Theorem in this problem.
Given sides a, b, and c, a triangle exists if:
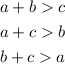
If each of these inequalities hold, we can say that the triangle does, in fact, exist.
The quickest way to test any triangle is to add the shortest side and the medium side to determine if their sum is greater than the longest side.
Option 1: 15, 17, 25
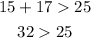
15, 17, 25 is a triangle.
Option 2: 8, 15, 6
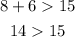
This is false.
Option 3: 19, 9, 13
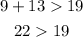
19, 9, 13 is a triangle.
Option 4: 24, 15, 33
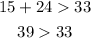
24, 15, 33 is a triangle.
Option 5: 9, 21, 29
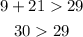
9, 21, 29 is a triangle.
Option 6: 3, 7, 10
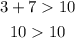
This is false.
The following groups of sides form triangles: 15, 17, 25; 19, 9, 13; 24, 15, 33; 9, 21, 29.