Given data:
Mass m1=9 kg
Mass m2=13 kg
To find:
Acceleration of the masses and the tension in the string for each system.
Solution:
By applying the newton's second law,
For mass m1, The equation can be written as,
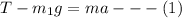
For the mass m2, the equation is
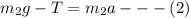
By adding these two equation we can get a formula to find acceleration,
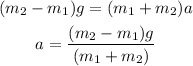
Here, by substituting the known values we can get
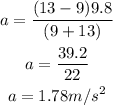
Thus the acceleration is 1.78m/s^2.
Now, to calculate the tension,
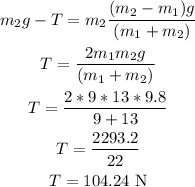
Thus, the tension in s string is 104.24 N