Given:
The scale from a playground to a scale drawing of the playground is 4 meters per centimeter.
The length of the playground= 5.3 cm.
The width of the playground = 3.8cm.
To find:
We need to find the area of the actual playground.
Step-by-step explanation:
The given ratio is
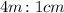
The length of the actual playground is
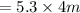
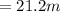
The length of the actual playground is l= 21.2m.
The width of the actual playground is
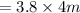
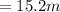
The width of the actual playground is w = 15.2m.
Consider the area of the rectangle.
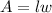
Substitute l=21.2 and w=15.2 in the formula.
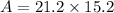
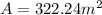
Final answer:
The area of the actual playground is 322.24 square meters.