Question

Make a sketch of the graph the absolute value equation. To earn full credit be sure to label; the increments on your x and y axis, the vertex as well as your intercepts. You can then take a picture of your handwritten work and upload it.f(x)=\frac{1}{2}|x+4|-3

Answer 1

vertex : (-4, -3)

x-intercept(s): (2,0), (-10,0)

y-intercept : (0, -1)

Step-by-step explanation

Given:

`f(x)=(1)/(2)|x+4|-3`

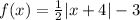
The vertex (h, k) is (-4, -3).

To graph, we need to first find the x and y-intercept.

To find the x-intercept, put f(x) =0 and solve for x

That is;

`0=(1)/(2)|x+4|-3`

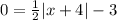
Add 3 to both-side of the equation

`(1)/(2)|x+4|=3`

Multiply both-side by 2

`|x+4|=6`

x+4 = 6 or x + 4 =-6

x= 6 - 4 x = -6 - 4

x=2 x = -10

Hence, the x-intercepts are (2,0) and (-10, 0)

To calculate the y-intercept, put x=0

That is;

`f(0)=(1)/(2)|0+4|-3`

`\begin{gathered} =(1)/(2)(4)-3 \\ \\ =2-3 \\ =-1 \end{gathered}`

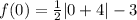
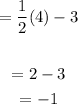
Hence, the y-intercept is (0, -1)