Question

Factor the given trinomial. If the trinomial cannot be factored, indicate “not factorable”X^2-2x-24

Answer 1

(x+4)(x-6)

Explanation:

Given the trinomial:

`x^2-2x-24`

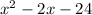
Factoring means we want an expression of the form: (x+_)(x+_).

To find the two numbers, we need two terms:

• Whose sum is the middle term, -2x

,

• Whose product is: -24x²

`\begin{gathered} -6x+4x=-2x \\ (-6x)(4x)=-24x^2 \end{gathered}`

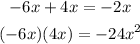
Replace the middle term with the sum.

`x^2-2x-24=x^2-6x+4x-24`

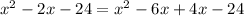
Next, group into two and factor it, ensuring that the expression inside the brackets is the same.

`\begin{gathered} =x(x-6)+4(x-6) \\ =(x+4)(x-6) \end{gathered}`

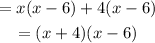
The factored form of the trinomial is (x+4)(x-6).