Question

Hi I’m having trouble I need help with this It’s from my ACT prep guide 21’ textbook

Answer 1

Hello there. To solve this question, we'll have to remember some properties about convergence of series.

Starting by the fact that for a given series:

`\sum ^(\infty)_(n=0)a_n`

We always take the limit to see whether or not:

`\lim _(n\to\infty)a_n=0`

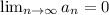
But in this case, we have to use the ratio test. Given two elements of the sequence we're adding the terms:

`\mleft\lbrace a_1,_{}a_2,\ldots,a_n,a_(n+1),\ldots,a_k\mright\rbrace_{}`

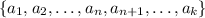
We say that for the following limit:

`\lim _(n\to\infty)\left|(a_(n+1))/(a_n)\right|=L`

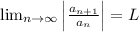
If L > 1, the series diverges by the ratio test.

If L = 1, the test is inconclusive.

If L < 1, the series converges by the ratio test.

In this case, the series is:

`(1)/(3^1)^{}+(2)/(3^2)+(3)/(3^3)+\ldots`

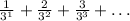
In which we can suppose that the general term is:

`a_n=\frac{n}{3^{n^{}}},n\ge1`

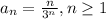
Hence we know that

`a_(n+1)=(n+1)/(3^(n+1)),n\ge1`

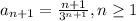
Now plugging in these terms in the ratio test, we have:

`\lim _(n\to\infty)\left|((n+1)/(3^(n+1)))/((n)/(3^n))\right|`

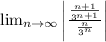
Knowing that:

`((a)/(b))/((c)/(d))=(a\cdot d)/(b\cdot c)`

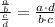
We have:

`\lim _(n\to\infty)\mleft|((n+1)\cdot3^n)/(3^(n+1)\cdot n)\right|\mright.`

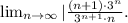
In which we can simplify the fraction by a factor 3^n