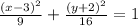Question

Write the equation of the ellipse in standard form that has vertices (3, 2) and (3, -6) and endpoints of the minor axis (0, -2) and (6, -2). Show all work.

Answer 1

The parts of the ellipse are:

In this case, we have:

• Vertices,: (3, 2) and (3, -6) → the vertices lie over the vertical line x = 3 → , the ellipse has the form of the ellipse at the ,right, in the graph,,

,

• Endpoints of minor axis,: (0, -2) and (6, -2).

In this case, the general equation of the ellipse is:

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1.`

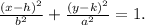
Where:

• (h, k) are the coordinates of the center of the ellipse,

,

• a and b are the legs.

From the graph at the right, we see that the equations for:

• the vertex are:

`\begin{cases}\mleft(h,k+a\mright)=\mleft(3,2\mright), \\ (h,k-a)=(3,-6)\text{.}\end{cases}`

We see that h = 3. Summing the equations and solving for k and a, we get:

`\begin{gathered} k+a=2,k-a=-6, \\ 2k=2-6=-4\Rightarrow k=-2, \\ -2+a=2\Rightarrow a=4. \end{gathered}`

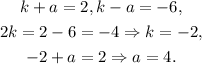
So we have a = 4 and k = -2.

• the endpoints of the minor axis are:

`\begin{gathered} (h+b,k)=(0,-2), \\ (h-b,k)=(-6,-2)\text{.} \end{gathered}`

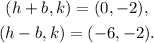
Solving for b and replacing the value h = -3, we get:

`h+b=0\Rightarrow b=-h\Rightarrow b=-(-3)=3.`

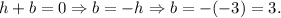
So we have b = 3.

The four parameters of the ellipse are:

• (h, k) = (3, -2),

,

• a = 4

,

• b = 3.

Replacing these values in the general equation of the ellipse, we get:

`\begin{gathered} ((x-3)^2)/(3^2)+((y+2)^2)/(4^2)=1, \\ \frac{(x-3)^2}{9^{}}+\frac{(y+2)^2}{16^{}}=1. \end{gathered}`

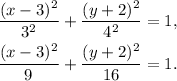
Answer

`\frac{(x-3)^2}{9^{}}+\frac{(y+2)^2}{16^{}}=1`