Given:
A company's marketing department has determined that if their product is sold at the price of p dollars per unit, they can sell q=1000−100p units. Each unit costs 7 dollars to make.
Required:
Solve part a and b.
Step-by-step explanation:
Part A.
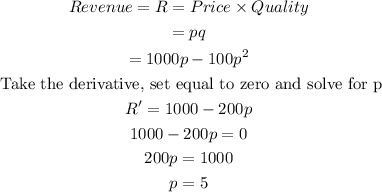
Part B.
To maximize profits, you need

Answer:
answered the question.