Answer
12
Explanation
The length of a segment with endpoints (x₁, y₁) and (x₂, y₂) is calculated as follows:
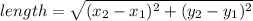
In this case, the endpoints are C(0,3) and D(0,7), then the length of the segment CD is:
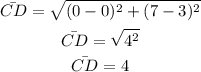
After CD is dilated by a factor of 3, the length of the image will be:
