Let's list down the given data in the question.
radius = 10 meters
central angle = 7π/4
The formula in getting the area of the sector given radius and central angle in radian is:
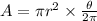
Since we have the value of the radius and angle in radian already, let's plug it in to the formula above. Use π = 3.14159
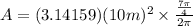
Then, solve.
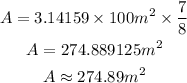
Hence, the area of the sector of circle given radius and angle is approximately 274.89 square meters.