Question

(1/3)^x=18 can you compute this

Answer 1

We have the following equation,

`((1)/(3))^x=18`

By taking logarithm base 3 to both sides, we have

`\log _3((1)/(3))^x=\log _318`

By the powers rule for logarithms, we get

`x\cdot\log _3((1)/(3))^{}=\log _318`

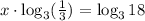
Now, by the quotient rule, we have that

`\begin{gathered} \log _3((1)/(3))=\log _3(1)-\log _3(3) \\ \log _3((1)/(3))=-\log _3(3) \end{gathered}`

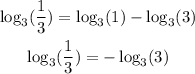
because base 3 logarithm of 1 is zero. Then, we have

`-x\cdot\log _3(3)^{}=\log _318`

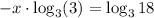
But

`\log _3(3)=1`

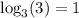
then, we obtain

`-x=\log _318`

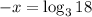
By multiplying both sides by -1, we have

`x=-\log _318`

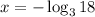
Finally, since

`\log _318=2.6309`

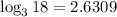
The answer is x= - 2.6309