We will have the following:
A) From this we will have that the angle will be given by:
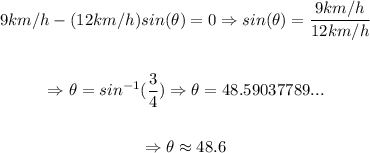
So, it must point approximately 48.6° upstream.
B) We will determine the time it takes to cross to the other side as follows:
First, we determine speed used to move to the other side:
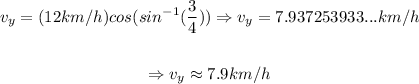
So, the time it will take to cross to the other side will be:
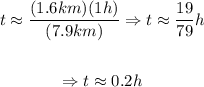
So, it will take approximately 0.2 hours; that is approximately 12 minutes.