Question

Exterior angle are supplementary to their adjacent interior angles

Answer 1

hello

to solve this question, we can simply use the theorem "angle on a straight line is equal to 180 degrees"

for the first polygon

to solve for x, y and z, we should simply subtract the adjacent interior angle from 180 degrees

`\begin{gathered} x+61=180 \\ x=180-61=119 \\ \end{gathered}`
`\begin{gathered} y+79=180 \\ y=180-79 \\ y=101 \end{gathered}`
`\begin{gathered} z+40=180 \\ z=180-40 \\ z=140 \end{gathered}`

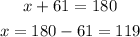
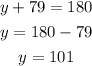
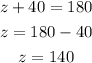
sum of exterior angles is

`119+101+140=360`

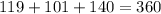
now we can proceed to the next polygon

now we can simply use the previous method for the last one

`\begin{gathered} a+124=180 \\ a=180-124=56 \end{gathered}`
`\begin{gathered} b+76=180 \\ b=180-79 \\ b=104 \end{gathered}`
`\begin{gathered} c+89=180 \\ c=180-89 \\ c=91 \end{gathered}`
`\begin{gathered} d+71=180 \\ d=180-71 \\ d=109 \end{gathered}`

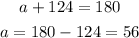
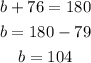
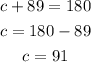
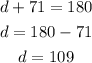
the sum of the exterior angles is

`56+104+91+109=360`

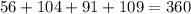
the next polygon is

then we proceed with the same method we've used before

`\begin{gathered} 98+a=180 \\ a=180-98 \\ a=82 \end{gathered}`
`\begin{gathered} b+121=180 \\ b=180-121 \\ b=59 \end{gathered}`
`\begin{gathered} c+87=180 \\ c=180-87 \\ c=93 \end{gathered}`
`\begin{gathered} d+130=180 \\ d=180-130 \\ d=50 \end{gathered}`
`\begin{gathered} e+104=180 \\ e=180-104 \\ e=76 \end{gathered}`

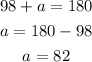
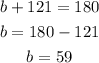
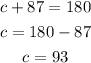
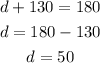
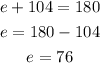
the sum of the exterior angles is

`82+59+93+50+76=360_{}`

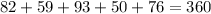
now we can solve for the last polygon

we can proceed to solve this through the previous method

`\begin{gathered} a+129=180 \\ a=180-129 \\ a=51 \end{gathered}`
`\begin{gathered} b+124=180 \\ b=180-124 \\ b=56 \end{gathered}`
`\begin{gathered} c+112=180 \\ c=180-112 \\ c=68 \end{gathered}`
`\begin{gathered} d+123=180 \\ d=180-123 \\ d=57 \end{gathered}`
`\begin{gathered} e+117=180 \\ e=180-117 \\ e=63 \end{gathered}`
`\begin{gathered} f+115=180 \\ f=180-115 \\ f=65 \end{gathered}`

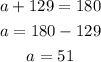
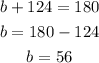
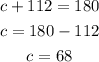
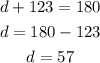
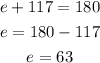
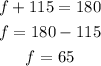
the sum of the exterior polygons is

`51+56+68+57+63+65=360`

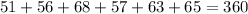
the sum of all the exterior angles of a regular polygon is equal to 360 degrees