Question

Assume the helium-neon lasers commonly used in student physics laboratories have power outputs of 0.250 mW.(a) If such a laser beam is projected onto a circular spot 2.50 mm in diameter, what is its intensity (in watts per meter squared)? W/m2(b) Find the peak magnetic field strength (in teslas). T(c) Find the peak electric field strength (in volts per meter). V/m

Answer 1

ANSWERS

(a) I = 50.92 W/m²

(b) B₀ = 6.53 x 10⁻⁷ T

(c) E₀ = 195.9 V/m

Step-by-step explanation

Given:

• the power output of a helium-neon laser, P = 0.250 mW = 2.5 x 10⁻⁴ W

Find:

• (a), The intensity, I in W/m², if a laser beam is projected into a circular spot with a diameter d = 2.50 mm

,

• (b), The peak magnetic field strength, B₀ in T

,

• (c), The peak electric field strength, E₀ in V/m

(a) The intensity of a beam of light of power P projected in area A is,

`I=(P)/(A)`

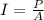
We know that the circular spot has a diameter of 2.50 mm, so its radius is,

`r=(d)/(2)=(2.50mm)/(2)=1.25mm=1.25\cdot10^(-3)m`

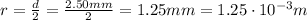
So, the area of the circular spot is,

`A=\pi r^2=\pi\cdot(1.25\cdot10^(-3))^2m^2\approx4.91\cdot10^(-6)m^2`

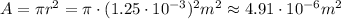
And the intensity is,

`I=(P)/(A)=(2.5\cdot10^(-4)W)/(4.91\cdot10^(-6)m^2)\approx50.92W/m^2`

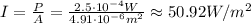
Hence, the intensity of the laser beam is 50.92 W/m², rounded to two decimal places.

(b) The intensity of the beam is also related to the peak magnetic field as follows,

`I=(c\cdot B_0^2)/(2\mu_0)`

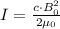
Where c is the speed of light, 3 x 10⁸ m/s, and μ₀ is the vacuum magnetic permeability, 1.257 x 10⁻⁶ H/m.

Solving this equation for B₀,

`B_0=\sqrt{(2I\mu_0)/(c)}=\sqrt{(2\cdot50.92W/m^2\cdot1.257\cdot10^(-6)H/m)/(3\cdot10^8m/s)}\approx6.53\cdot10^(-7)T`

Hence, the peak magnetic field strength is 6.53 x 10⁻⁷ T.

(c) The peak electric field strength is proportional to the peak magnetic field strength. The constant of proportionality is the speed of light,

`E_0=cB_0`

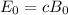
Using the peak magnetic field strength found in part (b),

`E_0=3\cdot10^8m/s\cdot6.53\cdot10^(-7)T\approx195.9V/m`

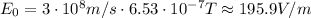
Hence, the peak electric field strength is 195.9 V/m.