Question

Amy and Allison are both running toward the soccer ball during a game.Amy's path is represented by the parametric equations x(t)=40 + 2/3t, y(t) = 6 + 1/6t, where t is on the interval [0,50] and t is measured in tenths of seconds.Allison's path is represented by the parametric equations x(t)=12 + 2t, y(t)= 5+ 1/4t, where t is on the interval [0,50] and t is measured in tenths of seconds.

Answer 1

They never collide.

Step-by-step explanation:

We have the equations:

`\begin{gathered} Amy\begin{cases}x(t)=40+(2)/(3)t \\ y(t)={6+(1)/(6)}t\end{cases} \\ Allison\begin{cases}x(t)={12+2t} \\ y(t)={5+(1)/(4)t,}\end{cases} \end{gathered}`

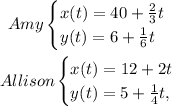
If the two girsl collide at a certain t, then

`\begin{gathered} x_(Amy)(t)=x_(Allison)(t) \\ y_(Amy)(t)=y_(All\imaginaryI son)(t) \end{gathered}`

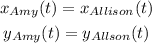
Then, we can equal each pair of euqations to find if there is any time t when their positions are the same.

Then:

`x_(Amy)(t)=x_(All\imaginaryI son)(t)\Rightarrow40+(2)/(3)t={12+2t}`

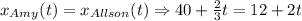
And solve for t:

`\begin{gathered} 40+(2)/(3)t=12+2t \\ 40-12=2t-(2)/(3)t \\ 28=(4)/(3)t \\ t=28÷(4)/(3)=28\cdot(3)/(4) \\ t=21s \end{gathered}`

Now, if the girls collide, at t = 21s they will be at the same place in in y(t)

Let's see:

`y_(Amy)(21s)={6+(1)/(6)}\cdot21`

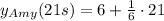
And solve:

`y_(Amy)(21s)=6+(7)/(2)=9.5`

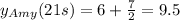
Now, for Allison:

`y_{All\mathrm{i}son}(21)=5+(1)/(4)\cdot21`

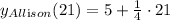
And solve:

`y_(All\imaginaryI son)(21)=5+5.25=10.25`

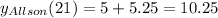
Then, we have:

At t = 21s the two girls are at the same position in the x axis. But, at 21s, in the y axis, Amy is at 9.5 and Allison at 10.25

To collide, they have to be in the same position in the x and y axis at the same time.

Thus, they never collide.