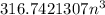Question

You are making party hats like the ones below that are shaped like cones. The finished hats will be 10 inches tall and have a diameter of 5.2 inches. How much material do you need to create three party hats?Show your work and final answer. Use 3.14 for pi

Answer 1

To solve this problem, we will compute the surface area of one cone and multiply it by 3.

Recall that the surface area of a cone is given by:

`SA=πr\left(r+√(h^2+r^2)\right),`

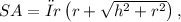
where r is the radius of the cone, and h is its height.

Now, in the given problem:

`\begin{gathered} r=(5.2)/(2)in=2.6in, \\ h=10\text{ in.} \end{gathered}`

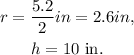
Therefore, the surface area of one cone is:

`SA=3.14(2.6in)(2.6in+√((2.6in)^2+(10in)^2).`

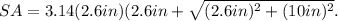
Simplifying the above result, we get:

`SA=105.5807102in^3.`

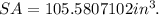
Finally, multiplying the above result by 3, we get:

`316.7421307in^3.`

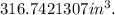
Answer:

`316.7421307\imaginaryI n^3`