Question

The figure shows the graph of f(x)=4+x/x+3, along with it's tangent line at the point (0,4). What is f'(0)?

Answer 1

Since we know the tangen line:

`y=(1)/(3)x+4`

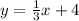
then f ^prime evaluated at zero is the same as evaluate this last equation at x=0, that is,

`f\text{´}(0)=(1)/(3)(0)+4`

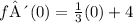
which gives

`f^(\prime)(0)=4`

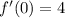
then, the answer is 4.

Lets compute the derivative of our given function:

then, f^prime at zero is equal to

then, the answer is 1/3. Then, the given line doesnt correspond with the derivative at x=0