Question

Solve the compound inequality 3r + 2 < 5 or 7r - 10 > 60

Answer 1

Inequalities

We have the inequalities

3r + 2 < 5

7r - 10 > 60

The solution of this system comes from the first solution combined with the second solution through an OR operator.

It means the solution can be in the first or in the second inequality

solving the first inequality:

3r + 2 < 5

Subtracting 2:

3r < 5 - 2

3r < 3

Solving:

r < 1

This means any number less than 1 is part of the solution

Solving the second inequality:

7r - 10 > 60

Adding 10:

7r > 60 + 10

7r > 70

Solving:

r > 70/7

r > 10

This means that every number greater than 10 is also part of the solution

Collecting both parts:

`r\in(-\infty,1)\text{ }\cup(10,+\infty)`

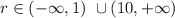
That is the solution in interval form

The interval form gives the solution when the variable belongs to an interval

In general, an interval has the form (a,b), where a is the left endpoint and b is the right endpoint. In this case, none of them is included in the solution

If a was included, then the interval was [a,b)

It both were included, the interval would be [a,b]

If any endpoint has no limit, we use parentheses and the infinity sign