To solve this question, we need to visualize the wheel. See below:
The motion f the pot is clearly a cosine motion, the minimum height is 0 instead of -12, so we can see that the cosine function has been shifted up by 12 units, so our equation is;
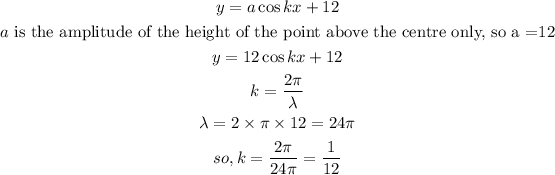
Thus, the complete equation is;
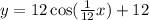
That is Option D