We have a deposit of $4000 at the end of each year.
The rate is 5% compounded annually (r = 0.05).
The number of periods is n = 10.
We have to calculate the present value of the annuity.
We will use the formula:
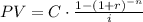
If we replace with our data, we get:

Now, we have to calculate the interest.