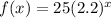
One way to solve this is to fit the choices into the function
Let's take choice no.3 to illustrate how it is done.
(1 , 55)
Meaning if x = 1 , f(x) must be 55.
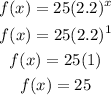
so if x = 1, then f (x) is 25. Therefore, choice number 3 is NOT the answer.
Let's take choice no. 2.
(0.5, 37.08)
Meaning if we substitute 0.5 in x, we have to get 37.08 as the value of f(x).
Let's see.
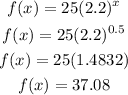
If x = 0.5, f(x) = 37.08. Therefore choice 2 is a CORRECT answer
Let's try the other choices , to checkif there are more than one correct answer
Let's take choice no.1
( 0.0)
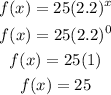
choice number 1 is NOT the answer.
Lastly, choice n0.4
(2,121)
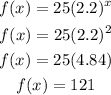
If x = 2, f(x) = 121. Therefore choice 4 is a CORRECT answer
Answers:
Choice 2 (0.5, 37.08)
Choice 4 (2, 121)